みんな嫌い！線路の計算問題

　若手社員など、カントやロングレールの軸力について、よく計算させられたりしませんか？中には、苦手な人も多いかと思います。そこで、計算でよく出るパターンを語句の説明とともに整理しておきます。

---

均衡カント

　列車速度に対する遠心力を打ち消すための望ましいカントのこと。

• Ｃ＝Ｇ・ｖ²／ｇ・Ｒ[m]

　Ｃ：カント、Ｇ：軌間、ｖ：列車速度（Ｖ／3.6[m/s]）、ｇ：重力加速度（9.8[m/s²]）、Ｒ：曲線半径

　上式に軌間1067㎜（狭軌）、1435㎜（標準軌）、1500㎜（新幹線）を代入すると、それぞれ

• 在来線狭軌：Ｃ＝8.4×Ｖ²／Ｒ[㎜]
• 在来線標準軌：Ｃ＝11.3×Ｖ²／Ｒ[㎜]
• 新幹線：Ｃ＝11.8×Ｖ²／Ｒ[㎜]

　となります。

　　Ｃ：均衡カント[㎜]、Ｖ：列車速度[km/h]、Ｒ：曲線半径[m]

---

許容カント不足量

　望ましいカント（＝均衡カント）に対し、現場に設定するカント（＝設定カント）が小さいと、大きい遠心力が作用することとなります。なので、その差（＝カント不足量）が許容されるレベルかどうかを確認しないといけませんよね。

　余談ですが、列車は、同じ区間でも列車種別やダイヤによって速度は異なりますから、その都度、均衡カントがバラバラになります。したがって、設定にあたっては列車速度を速度ごとの本数で分け、二乗平均法で算出し１つの速度を割り出しています。

• Ｃ_ｄ＝Ｃ_ｍ－Ｃ_ｏ

　C_ｄ：カント不足量[㎜]、Ｃ_ｍ：均衡カント[㎜]、Ｃ_ｏ：設定カント[㎜]

　これが、さまざまな実験により在来線70㎜、新幹線90㎜まで許容できるなどと定められています。

　※ちなみに、実カントという言葉もありますが、これは現地のその時のカントという意味ですので、設定カントと混同しないようにしましょう。

---

緩和曲線長

　直線と円曲線を結ぶ曲線で、曲率、カント、スラックをてい減するために、列車速度やカント量に応じて十分な距離が必要です。このことから、次の条件の最大値以上の長さとしています。

• 車両の３点支持による脱線を避けるための安全限度（Ｌ₁）
• 列車速度に応じたカントの時間的な変化による乗心地限度（Ｌ₂）
• カント不足に伴って受ける過度な遠心力の時間的な変化による乗心地限度（Ｌ₃）

　速度によって異なりますが、それぞれ以下のとおりです。

（在来線狭軌）

• Ｌ₁＝300Ｃ_m ※解釈基準あり
• Ｌ₂＝10.0Ｃ_m・V（1,2級線）、8.0Ｃ_m・V（3級線）、7.0Ｃ_m・V（4級線）
• Ｌ₃＝9.0～7.0Ｃ_d・Ｖ

（在来線標準軌）

• Ｌ₁＝300Ｃ_m ※解釈基準あり
• Ｌ₂＝7.4Ｃ_m・V（1,2級線）、5.9Ｃ_m・V（3級線）、5.2Ｃ_m・V（4級線）
• Ｌ₃＝6.7～5.2Ｃ_d・Ｖ

（新幹線：G=1500㎜）※サイン半波長てい減

• Ｌ₁＝300Ｃ_m（V＜200km/h）・450Ｃ_m（V≧200km/h） ※解釈基準あり
• Ｌ₂＝7.1Ｃ_m・V（1,2級線）、5.7Ｃ_m・V（3級線）、5.0Ｃ_m・V（4級線）
• Ｌ₃＝6.4～5.0Ｃ_d・Ｖ

　Ｌ_n：緩和曲線長[m]、Ｃ_m：カント[m]、Ｖ：当該曲線の最高速度[km/h]、Ｃ_d：最大カント不足量[m]

↓「普通鉄道構造規則（運輸省令第14号）」に基づき運用される緩和曲線長

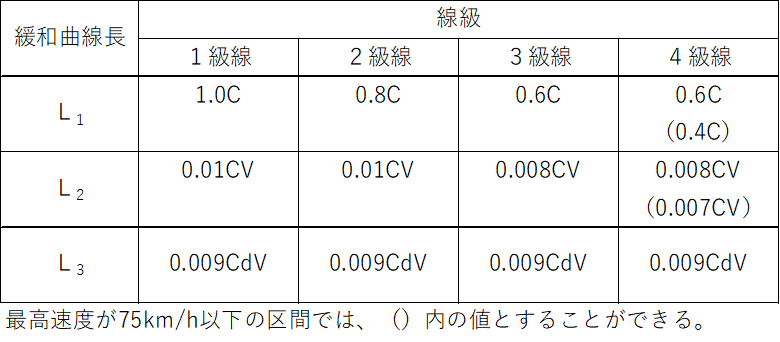
　Ｌ_n：緩和曲線長[m]、Ｃ：実カント[㎜]、Ｖ：当該曲線の最高速度[km/h]、Ｃ_d：最大カント不足量[㎜]

【緩和曲線の形状】

• ３次放物線（直線てい減）：曲率が緩和曲線始端における接線方向上のある横軸の点に対して直線的に比例する曲線。取扱いが容易なので、日本の鉄道の多くが用いている。
• レムニスケート曲線（直線てい減）：曲率が原点からの距離に対して直線的に比例する曲線。
• クロソイド曲線（直線てい減）：曲率が曲線上の距離に対して直線的に比例する曲線。急曲線でかつ緩和曲線長が短い一部の地下鉄で用いられている。
• サイン半波長（曲線てい減）：曲率とカントの変化が連続的な曲線。新幹線および一部の在来線高速線区で用いられている。

---

正矢

　曲線整正や現地の正しい正矢量を確認する際に、たまに計算したい場合がありますよね。ここで詰まらないよう、覚えておきましょう。

• Ｖ＝1000×Ｃ²／8Ｒ　※10m弦の場合：12500／Ｒで覚えると良い

　Ｖ：正矢量[㎜]、Ｃ：弦長[m]、Ｒ：曲線半径[m]

---

曲線区間における車両の偏いによる建築限界の拡大寸法

　車両が曲線区間を走行する際、軌道に対して車両の両端部は曲線外方に、中央部は曲線内方に偏いするので、曲線内外に建築限界を拡大する必要があります。また、カントがあれば、それによる偏いもあるので、併せて確認しておく必要があります。

【曲線による偏い量】

• Ｗ＝23100／Ｒ（在来線）
• Ｗ＝33450／Ｒ－34.5（R<300の曲線ホームがある場合）
• ω＝50000／Ｒ（新幹線）
• ω＝39000／Ｒ（新幹線の乗降場）

　W、ω：偏い量[㎜]、Ｒ：当該曲線半径[m]

【カントによる傾斜に伴う幅の加算寸法】

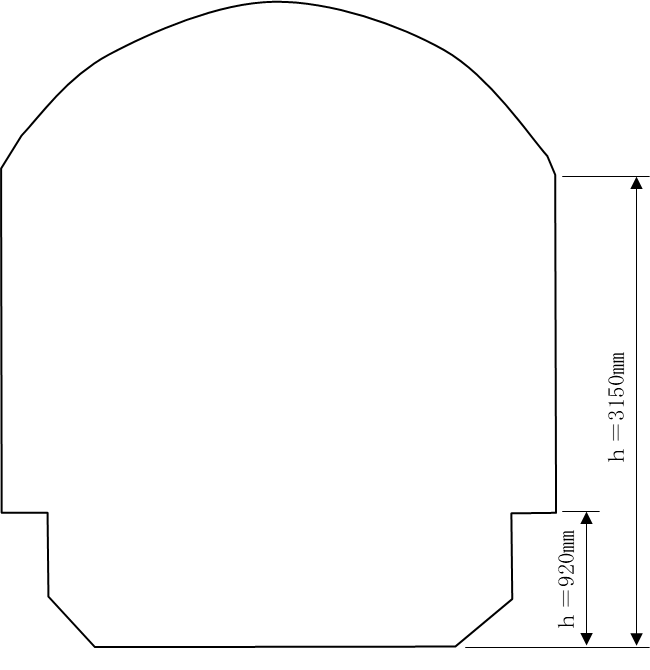
• ΔＷ＝ｈ×ｃ／Ｇ
• ｄ＝2.95×ｃ
• ｅ＝0.86×ｃ

　ΔW：偏い量[㎜]、ｈ：車両の端部の高さ[㎜]、ｃ：カント[㎜]、Ｇ：軌間[㎜]、ｄ：内軌側の最大の偏い量[㎜]、ｅ：外軌側の最小の偏い量[㎜]

　※ｈ＝3156（サイコロ）、920（国の）、Ｇ＝1067

【カントによる傾斜に伴う高さの加算寸法】

• 非電化区間：Δｈ＝Ｃ×1／2
• 電化区間：Δｈ＝Ｃ（直流）、Δｈ＝Ｃ×1／2（交流）

　Δｈ：カントによる余裕、Ｃ：カント[㎜]

---

偏いを考慮した軌道中心間隔

　https://track-mainte.com/construction を参照

---

遊間の安全管理

　遊間を管理する際、座屈側（目が詰まって張出す方）と破断側（目が開いてボルトが折れる方）の両方を管理する方法があります。それぞれ現場の遊間量を測定することで、危険度（＝安全率）を判定し、一定のラインを超えた箇所には必要な処置を行います。それぞれ計算方法を押さえましょう。

【座屈側の管理】

• ｅ＝Ｌ・β・Δｔ（自由伸縮量）よりΔｔ＝ｅ／Ｌ・β

　ｅ：設定遊間[㎜]、Ｌ：前後の平均レール長[m]、β：線膨張係数[/℃]、Δｔ：温度差[℃]

• α＝Ｐ／Ｐ_t
• Ｐ＝Ｅ・Ａ・β・Δｔ＝Ｅ・Ａ・β・（ｔ_max－ｔ－Δｔ）＝Ｅ・Ａ・β・（ｔ_max－ｔ－ｅ₀／Ｌ・β）
• ｅ₀＝ｙ±修正遊間量（温度上昇時はマイナス、下降時はプラス）

　　※最低座屈強度は軌道環境による道床横抵抗力、曲線半径によって異なる

　　※修正遊間量：継目板拘束力により蓄積された軸力の遊間換算量

• 前後のレールが35m未満：±1㎜
• 片方のレールが35m未満と35m以上：±2.5㎜
• 前後のレールが35m以上：±4㎜

　α：安全率、Ｐ：発生軸力[kgf]、Ｐ_t：最低座屈強度[kgf]、Ｅ：弾性係数（ヤング係数）[kgf/cm²]、Ａ：レールの断面積[cm²]、ｔ_max：予想最高レール温度[℃]、ｔ：遊間設定時のレール温度[℃]、ｅ₀：前後３継目の修正遊間平均値[㎜]、ｙ：現場の遊間量[㎜]

　※Ｅ＝2.1×10⁶、Ａ＝77.5（60K）、64.2（50N）、β：1.14×10^-5、ｔ_max：60

　上記により各継目の安全率を求め、５継目連続が下記の値を超える場合、

• Ｃランク：α≧0.90　⇒酷暑期までに遊間整正
• Ｂランク：0.90>α≧0.75　⇒遊間整正や監視など
• Ａランク：0.75>α　⇒遊間整正や監視など

　※５継目連続を超える条件は、規定遊間との差が2㎜を超える場合や安全率が0.65を超える場合など、鉄道事業者により異なっている。

（参考：規定遊間の算出式）

• ｅ＝45・β・Ｌ−β・ｔ・Ｌ

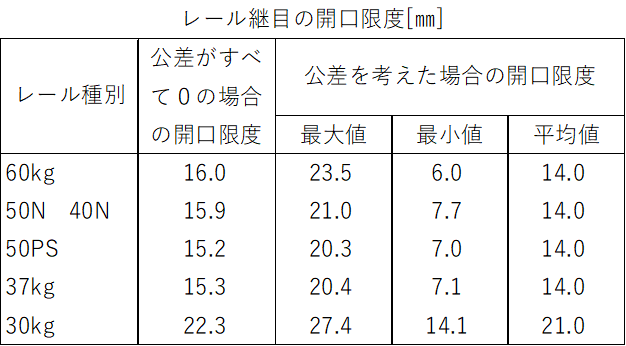
【破断側の管理】

• Ａ限度（注意限度）：ボルトの塑性変形を全く許容しない限度（約50kN）→ｅ_max＝15.3㎜
• Ｂ限度（必要限度）：1本のボルトに1～2㎜程度の塑性変形を許容する限度（約100kN）→ｅ_max＝16.3㎜
• Ｃ限度（安全限度）：2本のボルトのうち1本に対して、大きな塑性変形または折損を許容する限度（約150kN）→ｅ_max＝17.3㎜

　※30kgレールのみ、ｅ_max＝21.7㎜として良い

　ｅ_max：開きうる遊間の限度（５継目平均）[㎜]

　上記限度のうち、Ａ限度はリスクが低く無視できるものとし、Ｂ限度以上、Ｃ限度以上に対して必要な処置を行うものとしています。

（必要な処置の例）

• Ｃ限度以上（Ｌランクと表す事業者もある）：遊間整正など
• Ｂ限度以上（Ｍランクと表す事業者もある）：継目ボルト締め直し、継目ボルト交換、アンチクリーパの増設、遊間整正など

【参考目安値】

---

ロングレール安全度

　道床状態に不備があったり、列車の制動によりレールのふく進があったり、締結装置の不良で所定の抵抗力がなかったりした場合に、ロングレールの座屈（張出し）や破断（折損）が発生する場合があります。特に、座屈に対しては、その挙動を把握し事前に整備する必要があります。以下は、ロングレール設定替を行う目安として、安全度を計算する方法を記述しておきます。

• Ｐ＝Ｅ・Ａ・β・Δｔ（不動区間の発生軸力）
• 簡易式Ｐ＝1.54Δｔ（50N）、1.86Δｔ（60K）※この場合の単位はｔ

　Ｐ：発生軸力[kgf]、Ｅ：弾性係数（ヤング係数）[kgf/cm²]、Ａ：レールの断面積[cm²]、β：線膨張係数[/℃]、Δｔ：設定温度からの差[℃]

　※Ｅ＝2.1×10⁶、Ａ＝77.5（60K）、64.2（50N）、β：1.14×10^-5

• Δｔ＝Δｔ₁＋Δｔ₂＋Δｔ₃（Δｔ<0の場合、Δｔ＝0とする）
• Δｔ₁＝ｔ_min－ｔ₀ （Δｔ₁が負の場合－5℃を限度とする）
• Δｔ₂＝（ｔ₀－ｔ₂）/2 ※可動区間のレール交換
• Δｔ₂＝ｔ₀－ｔ₂ ※不動区間のレール交換
• Δｔ₃＝88×Ｓ/Ｌ（伸びの場合Δｔ₃＝0とする）
• α＝Ｐ_tmin／Ｐ_max＝1.2ｉ^0.521×1/（1+Δｔ/Δｔ^N_max）

　Δｔ：換算負荷温度[℃]、Δｔ₁：設定温度よりも低いことによる[℃]、Δｔ₂：低温時作業による[℃]、Δｔ₃：ふく進状態による[℃]、ｔ_min：許容最低設定温度[℃]、ｔ₀：設定温度[℃]、ｔ₂：作業時のレール温度[℃]、Ｓ：ふく進杭間の縮み量[㎜]、Ｌ：ふく進杭の間隔[m]、α：安全度、Ｐ_tmin：最低座屈強度[kgf]、Ｐ_max：最大軸力[kgf]、ｉ：道床横抵抗力比、Δｔ^N_max：最大レール温度差[℃]

　※安全度（甲）：道床整備を行う前の安全度、安全度（乙）：道床整備を行った後の安全度、ｉ＝1.2（道床横抵抗力を500kgf/m以上確保すべき時は1.0）、Δｔ^N_max＝35（道床横抵抗力を500kgf/m以上確保できる場合は40）

　∴安全度（乙）＜1.2の場合は、設定替などの整備を検討する

【参考目安値】

• 通常の軸力は最大でも60tf程度である

---

レール破断時の開口量

　走行安全性の実験から開口量の限度値が定められました。そこで無道床橋梁長は50m以下が望ましいとされていました。開口量の計算は日常業務で計算する場面は少ないかもしれません。しかしながら、橋上ロングレール化を図ろうとするとき、可否の検討を行う必要があります。橋梁として縦荷重を与えても良いか、どの程度耐えうるか、ロングレールの座屈に対する抵抗力は十分か、破断時の開口量は70㎜以下となるか等を検討します。検討する際は、ＥＪの有無や位置、締結装置の種類などの情報を専用のシステムに入力して判断することが一般的だと思いますが、基本的な理論として知っておくと良いでしょう。

• Ｌ₀＝Ｐ／γ＝Ｅ・Ａ・β・Δｔ／γ（ロングレールの可動区間長）
• ｙ＝（Ｌ₀・Ｐ／２）／Ｅ・Ａ＝Ｅ・Ａ・β²・Δｔ²／２・γ（ロングレール端部の伸び量）
• Ｓ＝２・ｙ＝Ｅ・Ａ・β²・Δｔ²／γ（ロングレール破断時の開口量）

　※開口量はロングレールの端部2つの伸び量の合計と同じなので2倍

• ｅ＝Ｌ・β・Δｔ＋Ｓ（無道床橋梁内での開口量） ≦ 70㎜となるように

　※無道床橋梁内は原則、縦抵抗力を0とするため、自由伸縮量＋有道床部の破断量となる

　Ｌ₀：可動区間長[m]、Ｐ：発生軸力[kgf]、γ：道床縦抵抗力[kgf/cm]、Ｅ：弾性係数（ヤング係数）[kgf/cm²]、Ａ：レールの断面積[cm²]、β：線膨張係数[/℃]、Δｔ：設定温度からの差[℃]、ｙ：端部の伸び量[㎜]、Ｓ：破断時の開口量[㎜]、ｅ：破断時の開口量（無道床橋梁）[㎜]

　※γ＝400～800（在来線）、900～1000（新幹線）（道床横抵抗力の1.5～2.0倍）、Ｅ＝2.1×10⁶、Ａ＝77.5（60K）、64.2（50N）、β：1.14×10^-5

【参考目安値】

• 温度変化によるEJ端部の伸縮量（有道床部）：約±25㎜以下

---

（参考文献）

• 解説 鉄道に関する技術基準（土木編）第四版
• 保線工学<上>
• 保線問答集（下巻）　鉄道現業社 編